En la materia de Ecuaciones Diferenciales, dirigida por el maestro Alonso Jacobo, los estudiantes culminaron su curso con un ambicioso proyecto final enfocado en la implementación de métodos numéricos para mostrar el dominio de ecuaciones con codificaciones en Python y C#.
Los alumnos desarrollaron códigos para los métodos de Euler, Euler Mejorado y Runge-Kutta, con el objetivo de analizar y comparar la precisión de estos métodos mediante gráficas y curvas lineales.
Objetivo del Proyecto
El principal objetivo del proyecto fue proporcionar a los estudiantes una comprensión práctica y profunda de cómo los métodos numéricos pueden ser utilizados para aproximar soluciones de ecuaciones diferenciales.
Mediante la codificación de los métodos de Euler, Euler Mejorado y Runge-Kutta, se buscó:
- Mejora Continua en la Resolución de Ecuaciones: Permitir a los estudiantes comparar la efectividad y precisión de cada método.
- Visualización de Resultados: Utilizar gráficas y curvas lineales para visualizar las trayectorias de las soluciones y determinar cuál método se aproxima más a la solución exacta.
- Desarrollo de Habilidades de Programación: Fortalecer las habilidades en programación, específicamente en Python y C#.
Métodos Implementados
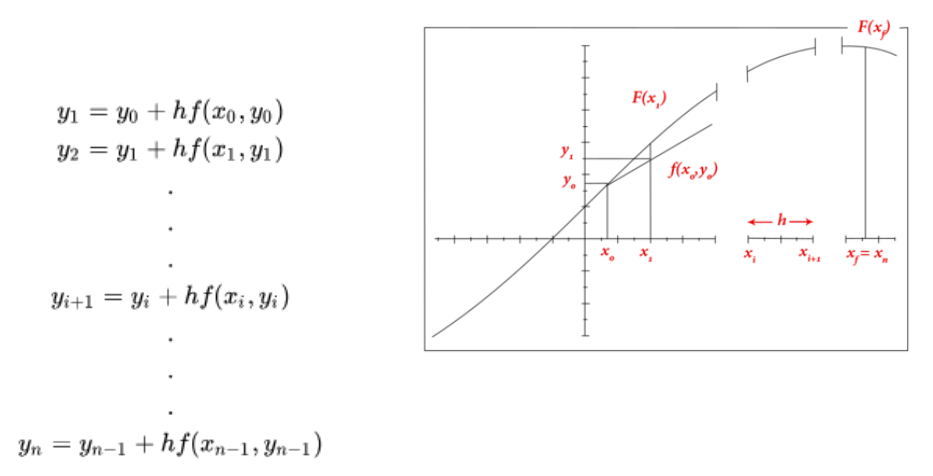
- Método de Euler:
- Descripción: Es el método más básico para la resolución numérica de ecuaciones diferenciales. Aproxima la solución usando la pendiente de la función en el punto inicial.
- Implementación: Los estudiantes codificaron el método de Euler en Python y C#, creando scripts que calculaban y graficaban las soluciones aproximadas.
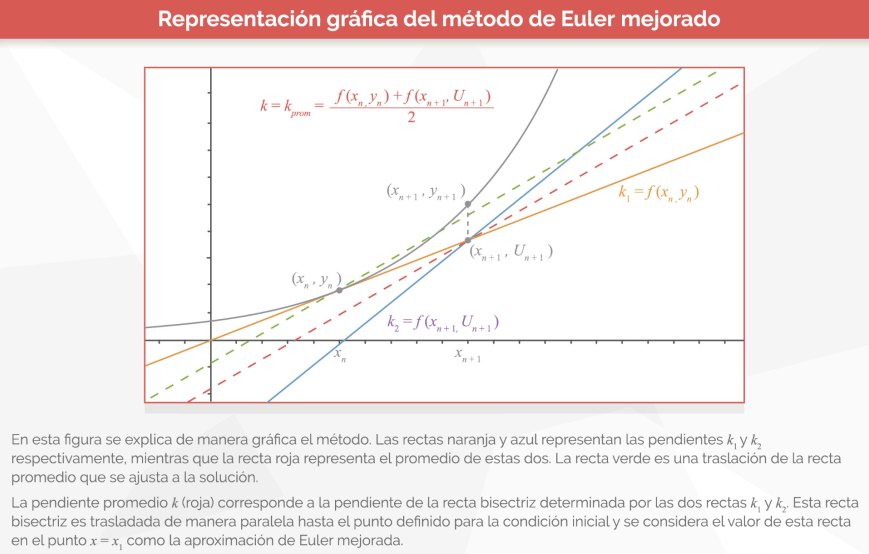
- Método de Euler Mejorado:
- Descripción: También conocido como el método del punto medio, mejora la precisión del método de Euler al considerar la pendiente en el punto medio del intervalo.
- Implementación: Los códigos desarrollados en Python y C# utilizaron este método para calcular soluciones más precisas que las obtenidas con el método de Euler simple.
- Método de Runge-Kutta:
- Descripción: Es uno de los métodos más utilizados debido a su alta precisión. Los estudiantes implementaron la versión de cuarto orden, que es la más común.
- Implementación: Los scripts en Python y C# incluyeron el método de Runge-Kutta de cuarto orden, permitiendo comparar su exactitud con los métodos de Euler y Euler Mejorado.
Visualización y Comparación
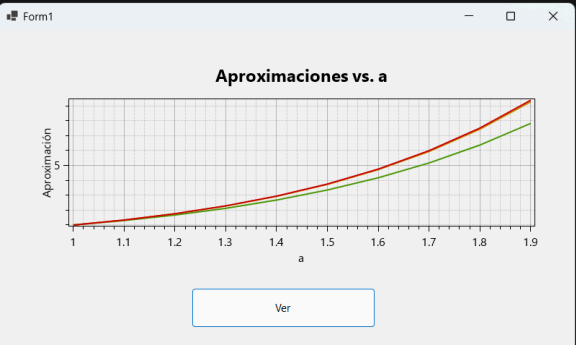
Para evaluar la precisión de cada método, los estudiantes generaron gráficas y curvas lineales que mostraban las trayectorias de las soluciones aproximadas en comparación con la solución exacta de las ecuaciones diferenciales.
Estas visualizaciones permitieron:
- Identificación de Errores: Observar las diferencias entre las soluciones aproximadas y la solución exacta.
- Comparación de Métodos: Determinar cuál de los tres métodos se aproxima más a la solución exacta en diferentes escenarios.
- Análisis de Rendimiento: Evaluar el tiempo de ejecución y la eficiencia de cada método implementado en Python y C#.
Resultados y Aprendizajes
Los resultados del proyecto demostraron que el método de Runge-Kutta de cuarto orden proporciona la aproximación más precisa en comparación con los métodos de Euler y Euler Mejorado.
Sin embargo, los métodos de Euler y Euler Mejorado también mostraron ser efectivos en ciertos casos, especialmente cuando se requiere una solución rápida con menor carga computacional.
Aprendizajes Clave:
- Precisión de Métodos Numéricos: Comprensión de cómo y por qué los métodos de mayor orden, como Runge-Kutta, ofrecen mayor precisión.
- Programación en Python y C#: Fortalecimiento de habilidades en la implementación de algoritmos numéricos en lenguajes de programación populares.
- Análisis y Visualización de Datos: Importancia de la visualización gráfica para interpretar y analizar resultados matemáticos.
Conclusión
El proyecto final de los alumnos del maestro Alonso Jacobo en la materia de Ecuaciones Diferenciales ha sido un éxito rotundo.
A través de la implementación de métodos numéricos en Python y C#, los estudiantes no solo reforzaron sus conocimientos teóricos, sino que también adquirieron habilidades prácticas valiosas para su futuro profesional.
La capacidad de comparar y analizar la precisión de diferentes métodos numéricos, apoyada por visualizaciones gráficas, prepara a estos futuros ingenieros y científicos para enfrentar desafíos complejos en el ámbito de las matemáticas aplicadas y la programación.
Fuente: Trabajos de los alumnos
Ingeniería en Mecatrónica
Más noticias sobre Ingeniería en Mecatrónica

