Cálculo Integral visto desde su concepto y análisis matemático fundamental, implementado por los alumnos de Ingeniería.

Los orígenes del cálculo se remontan al menos 2500 años hasta los antiguos griegos, que encontraban áreas usando el “método de eliminaciones sucesivas.” Sabían cómo hallar el área A de cualquier polígono al dividirlo en triángulos y sumando las áreas de estos triángulos. Pero el problema empezaba a ser más difícil al hallar el área de una figura curva. El método griego de eliminaciones sucesivas era inscribir polígonos en la figura y circunscribir polígonos alrededor de la figura y luego aumentar el número de lados de los polígonos.

Sea An el área del polígono inscrito con n lados. A medida que n aumenta, se ve que An se acerca cada vez más al área del círculo. Entonces, decimos que el área del círculo es el límite de las áreas de los polígonos inscritos, y escribimos:
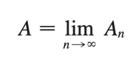
El método de los griegos
Los griegos mismos no usaron límites en forma explícita, pero por razonamiento indirecto, Eudoxio (siglo V a.C.) usó el método de eliminaciones sucesivas para demostrar la conocida fórmula para el área de un círculo: A = r2
La determinación del área es el problema central en la rama del cálculo llamada cálculo integral. El concepto de un límite surge al tratar de hallar el área de una región, la pendiente de una tangente a una curva, la velocidad de un auto, o la suma de una serie infinita. En cada caso el tema común es el cálculo de una cantidad como el límite de otras cantidades que se calculan con facilidad. Es la idea básica de un límite que separa al cálculo de otros campos de las matemáticas. De hecho, podríamos definir el cálculo como la parte de las matemáticas que se refiere a límites.
Ahora bien, sabemos que en matemáticas las operaciones tienen sus inversas; por ejemplo, la adición y la sustracción, la multiplicación y la división, elevar a una potencia y extraer una raíz, etcétera. En el cálculo integral sucede exactamente lo mismo; la integración es una operación inversa a la derivación. Después que Isaac Newton inventara su versión del cálculo, la utilizó para explicar el movimiento de los planetas alrededor del Sol.
Calculo Integral en la actualidad
Hoy el cálculo se emplea para calcular las órbitas de satélites y naves espaciales. Para predecir tamaños de población, estimar con qué rapidez suben o bajan precios del petróleo, para pronosticar condiciones atmosféricas, medir la respuesta cardiaca del corazón, calcular primas de seguros de vida, el volumen de un sólido, la longitud de una curva, la fuerza del agua contra una represa, la masa y centro de gravedad de una varilla, el trabajo realizado al sacar agua por bombeo de un tanque, y en una gran variedad de otros campos de actividad
Cálculo Integral
Entendiendo entonces que el Cálculo Integral es una de las herramientas más potentes y eficaces para estudiar diversos fenómenos. Este módulo en ESCAT está debidamente justificado al pretender que quienes lo estudien obtengan los conocimientos básicos del cálculo integral que le permitirán desarrollar en él las actitudes y habilidades necesarias en el planteamiento y solución de problemas que involucren el uso de estos conceptos.
Además, dentro de los propósitos está el que evalúe sistemas que representan un cambio, permitiéndolo predecir situaciones reales, formales y/o hipotéticas presentes en su contexto mediante el desarrollo de los métodos de integración. Esto contribuye en el desarrollo de su capacidad de razonamiento y toma de decisiones en diferentes ámbitos.
Escucha de nuestros estudiantes algunas de éstas aplicaciones en diferentes áreas:
Y así, tantas razones que justifican el cálculo integral como fundamento esencial en la formación del futuro profesional con bases suficientes para la relación interdisciplinaria con otras ramas tecnológicas y científicas.
Fuente: Mtra. García Gómez Alhelí
Asignatura: Cálculo Integral
Departamento de Ciencias
Ingenierías Uninter

