Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones desconocidas. Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se dividen en:
- Ecuaciones diferenciales ordinarias: aquellas que contienen derivadas respecto a una sola variable independiente.
- Ecuaciones en derivadas parciales: aquellas que contienen derivadas respecto a dos o más variables.

Por ejemplo se considera la ley, apoyada en experiencias, de que el radio se desintegra a una velocidad proporcional a la cantidad de radio presente, hecho que se describe

Es una que incluye expresiones o términos que involucran a una función matemática incógnita y sus derivadas. Algunos ejemplos de ecuaciones diferenciales son:

A la variable dependiente también se le llama función incógnita (desconocida). La resolución de ecuaciones diferenciales es un tipo de problema matemático que consiste en buscar una función que cumpla una determinada ecuación diferencial. Se puede llevar a cabo mediante un método específico para la ecuación diferencial en cuestión o mediante una transformada (como, por ejemplo, la transformada de Laplace).
Orden
El orden de la derivada más alta en una ecuación diferencial se denomina orden de la ecuación.
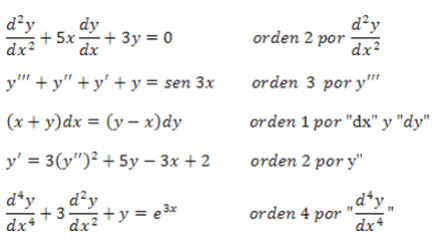
Grado
Es la potencia de la derivada de mayor orden que aparece en la ecuación, siempre y cuando esta esté en forma polinómica, de no ser así se considera que no tiene grado
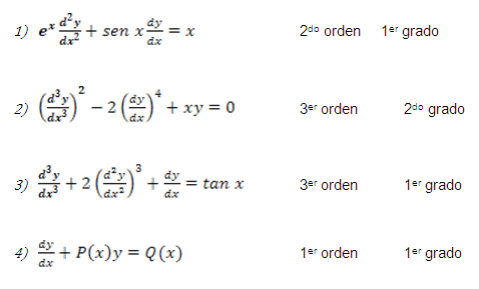
Ecuación diferencial lineal
Se dice que una ecuación es lineal si tiene la forma, es decir:
- Ni la función ni sus derivadas están elevadas a ninguna potencia distinta de uno o cero.
- En cada coeficiente que aparece multiplicándolas sólo interviene la variable independiente.
- Una combinación lineal de sus soluciones es también solución de la misma

Solución
Tipos de soluciones
Es una función que al reemplazar a la función incógnita, en cada caso con las derivaciones correspondientes, es verificar, es decir, la convierte en una identidad. Hay tres tipos de soluciones:
- Solución general: una solución de tipo genérico, expresada con una o más constantes.
Solución general
Es un haz de curvas. Tiene un orden de infinitud de acuerdo a su cantidad de constantes (una constante corresponde a una familia simplemente infinita, dos constantes a una familia doblemente infinita, etc.). En caso de que la ecuación sea lineal, la solución general se logra como combinación lineal de las soluciones (tantas como el orden) de la ecuación homogénea (que resulta de hacer el término no dependiente de ni de sus derivadas igual a 0) más una solución particular de la ecuación completa

Solución particular
Es un caso particular de la solución general, en donde la constante (o constantes) recibe un valor específico.
- Solución singular: una función que verifica la ecuación, pero que no se obtiene particularizando la solución general
Fuente: Dra. Alhelí García Gómez
Asignatura: Ecuaciones Diferenciales
Departamento de Ciencias
Ingenierías Uninter

