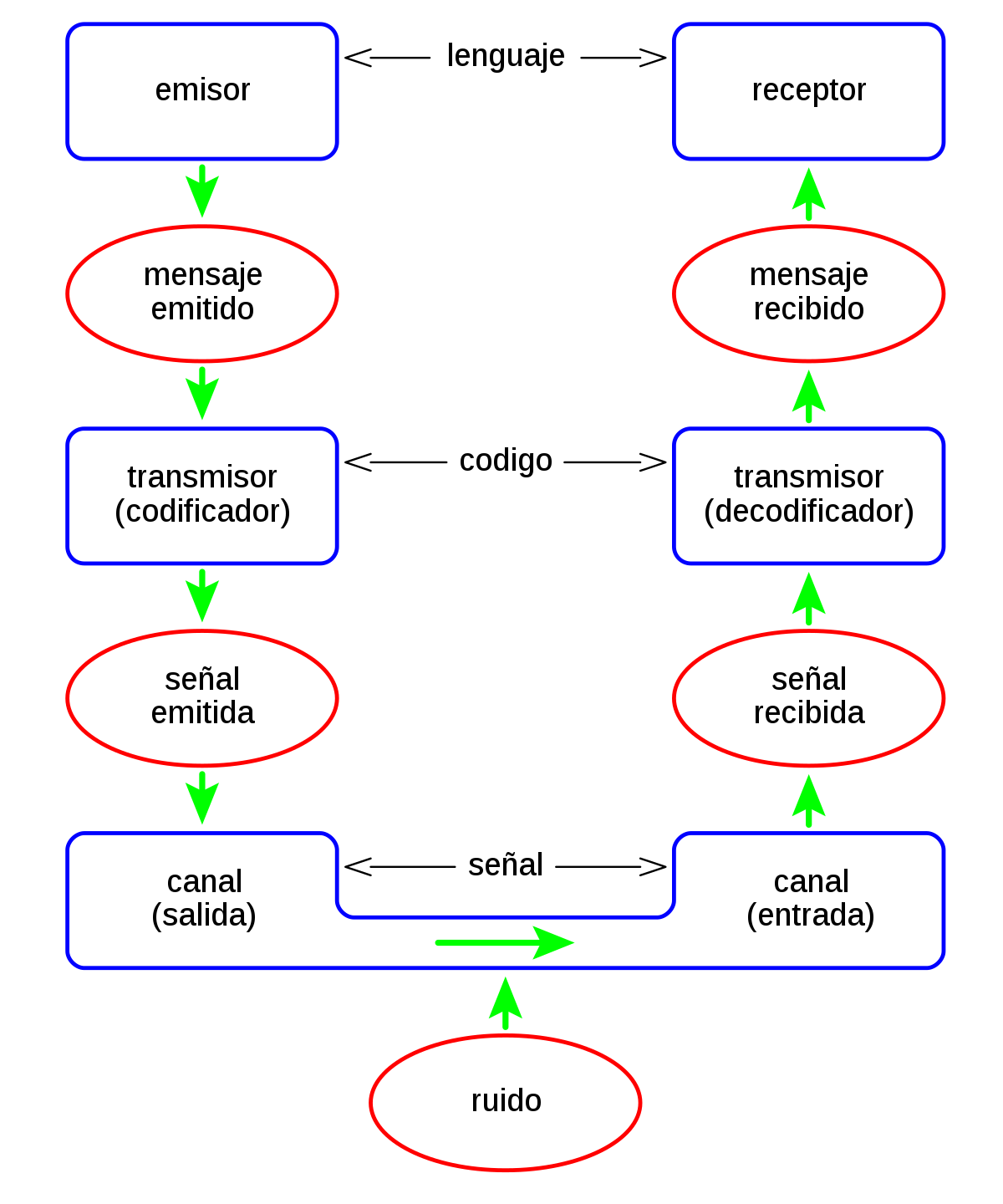
La teoría de la información, también conocida como teoría matemática de la comunicación, es un planteamiento que estudia el procesamiento y medición de datos en la transmisión de una información. El proceso de comunicación planteado por sus creadores establece el flujo de un mensaje entre un emisor y un receptor a través de un canal determinado.

La teoría de la información también se encarga de medir y representar la información, así como la capacidad de procesamiento de los sistemas de comunicación para transmitir dicha información. Es, además, una rama de la teoría de la probabilidad matemática. 

¿Cómo surge la teoría de la información?

La teoría matemática de la información fue propuesta en 1949 por el matemático e ingeniero Claude Shannon y el biólogo Warren Weaver. No obstante, es el resultado de investigaciones iniciadas casi treinta años antes por científicos como Andrei Markovi y Ralph Hartley, este último conocido por ser uno de los primeros representantes del lenguaje binario. 

El aporte de Alan Turing, quien llevó a cabo un esquema de una máquina capaz de procesar los datos de la información a través de emisiones de símbolos, fue el último precedente para el desarrollo, culminación y consagración de la que se llamó Teoría Matemática de la Comunicación.

Todos los estudios de la época tenían en común el mismo objetivo: buscar formas eficientes de utilizar canales de comunicación para enviar una información por medio de un canal sin que se viera afectada la calidad del mensaje que llegaba. 

¿Cuáles son los elementos de la teoría de la información?

1. Fuente de información o emisor: elemento capaz de emitir un mensaje. En la teoría de la información, las fuentes principales son:
   • Aleatorias: cuando el mensaje no se puede predecir.
   • Estructuradas: cuando hay cierto nivel de redundancia y orden.
   • No estructuradas: en la que todos los mensajes son aleatorios, sin relación ni sentido, por lo que hay una pérdida de parte del mensaje. 
2. Mensaje: se trata de un conjunto de datos que son transportados a través de un canal. 
3. Código: conjunto de elementos que siguen una serie de normas para su combinación, de manera que puedan ser interpretados. 
4. Canal: medio por el que se transmite el mensaje para que llegue al receptor. 
5. Información: es lo que se busca transmitir a través de un mensaje. Desde el punto de vista de la probabilidad matemática, marco teórico de la teoría de la información, la información debe ser proporcional al número de bits que se necesita para reconocer el mensaje.
6. Receptor o destinatario: quien recibe el mensaje. Es indispensable que sea capaz de asimilar el contenido del mensaje que se origina desde la fuente o emisor. 
7. Ruido: diferentes causas que impiden que el mensaje llegue con normalidad en el proceso de flujo de la información, de manera que el receptor no podrá entenderlo completamente.

¿Cuáles son los planteamientos generales de la teoría de la información?

• Sirve para estudiar el proceso informativo, como los posibles canales de comunicación y la comprensión de datos transferidos. 
• Determina la forma más sencilla y eficaz de transmitir un mensaje sin que haya alteraciones en el proceso. 
• Reconoce elementos de distorsión o impedimentos para que un mensaje llegue de manera óptima a un destinatario.  
• Establece que tanto emisor como receptor deben ser capaces de codificar y decodificar los mensajes. 
• Analiza la velocidad con la que se transmiten los mensajes. 
• Considera que un mensaje tiene múltiples sentidos, de manera que el destinatario lo dota de significado, siempre y cuando guarde el mismo código que el emisor. 
• Si la selección del mensaje se presenta entre dos únicas alternativas, el valor de la información es igual a uno (unidad denominada bit). Para que la información sea un bit, deben existir alternativas igual de probables en el proceso. Además, plantea que hay más información mientras más alternativas existan y todas sean igual de probables. 

¿Qué aplicaciones tiene la teoría de la información?

La teoría de la información representa una de las ramas más importantes de la matemática aplicada. Algunos de sus múltiples usos son:

• Ciencias de la computación, como la criptografía y la comprensión de datos.
• Ingeniería eléctrica, como la teoría de la comunicación y la teoría de la codificación.
• Estadística. 
• La biología, en el estudio de las secuencias de ADN y el código genético. 
• Pagos, transacciones electrónicas y procesos de autentificación. 
• Encriptación de mensajes o esteganografía.